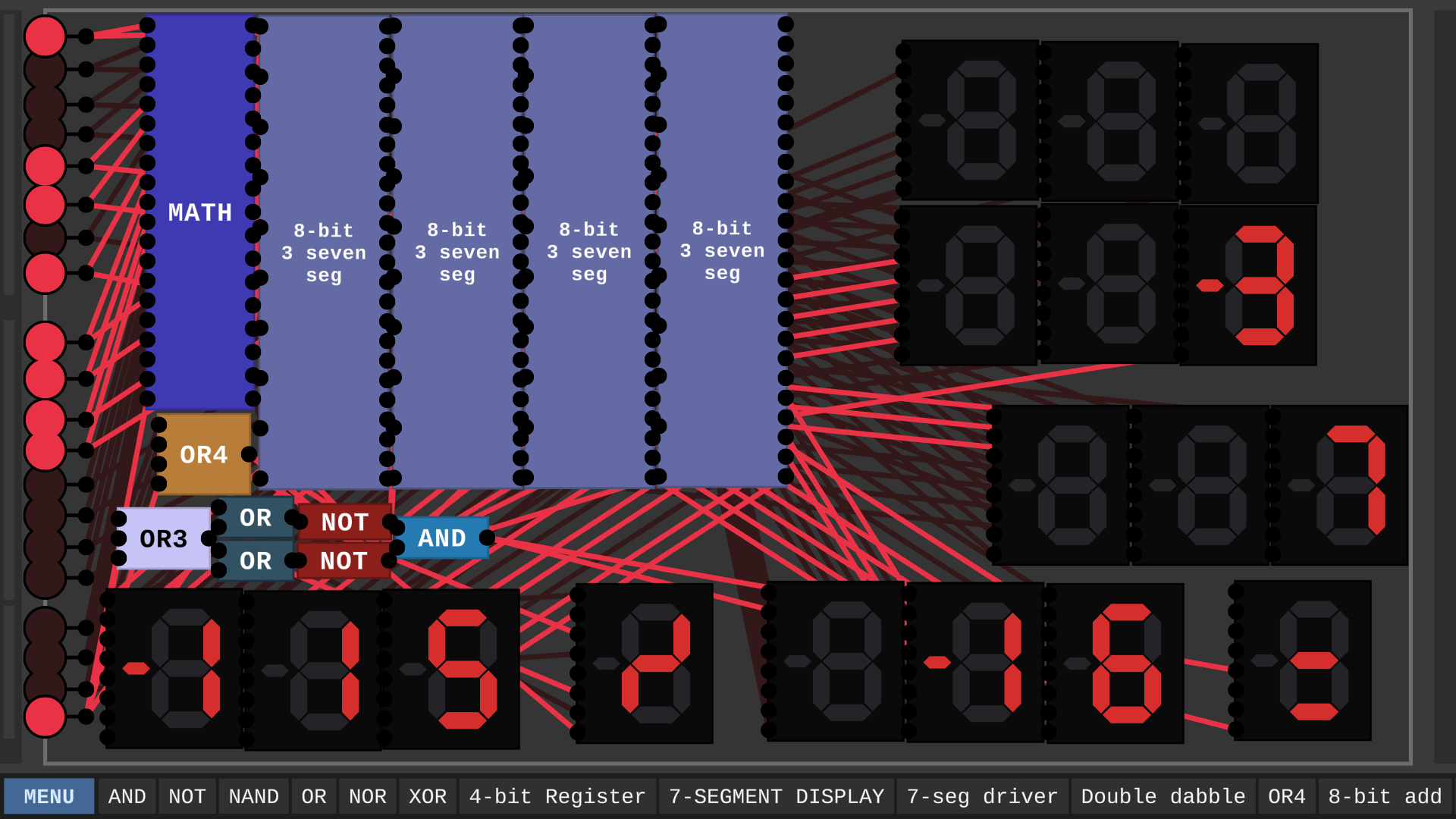
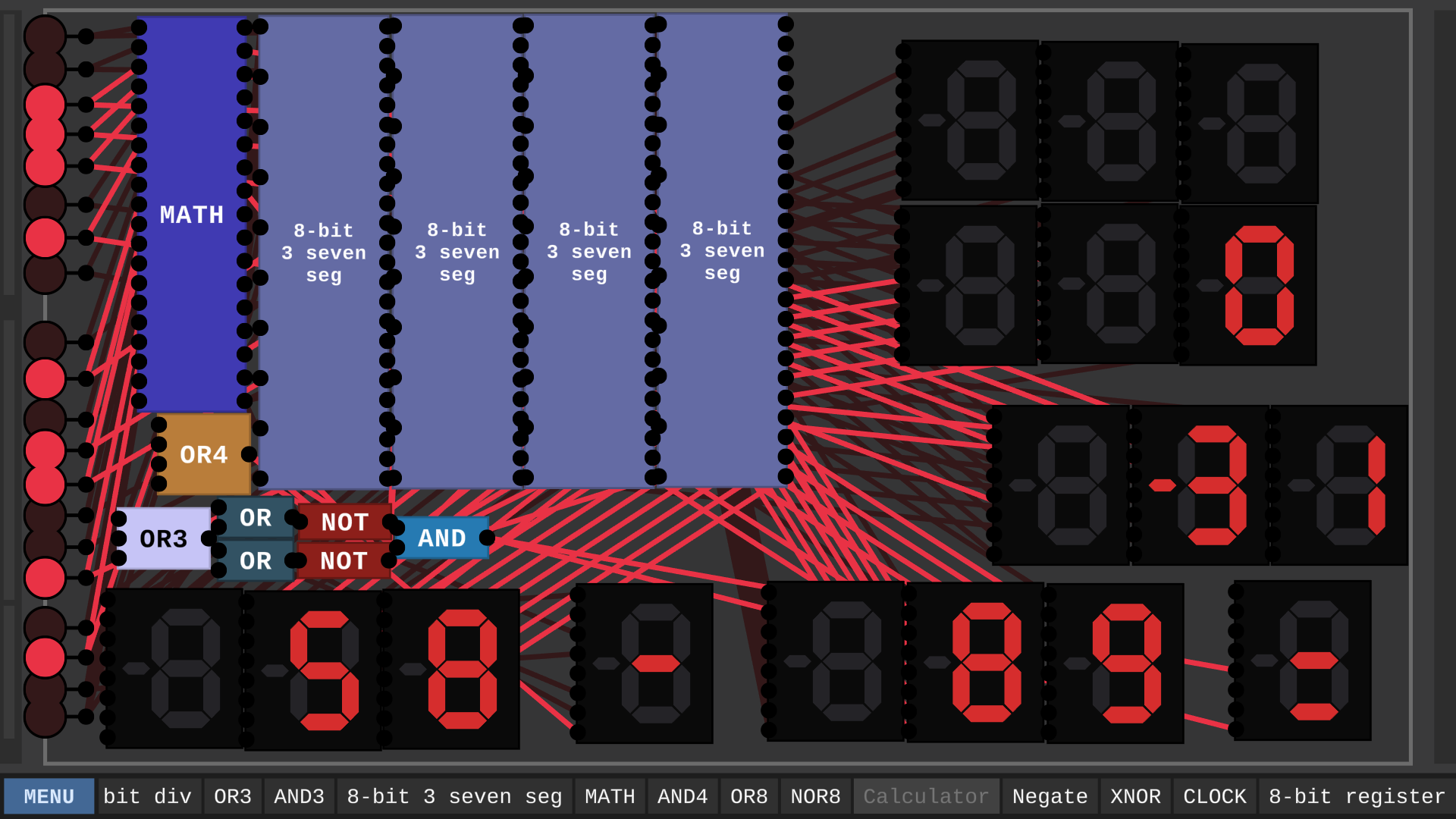
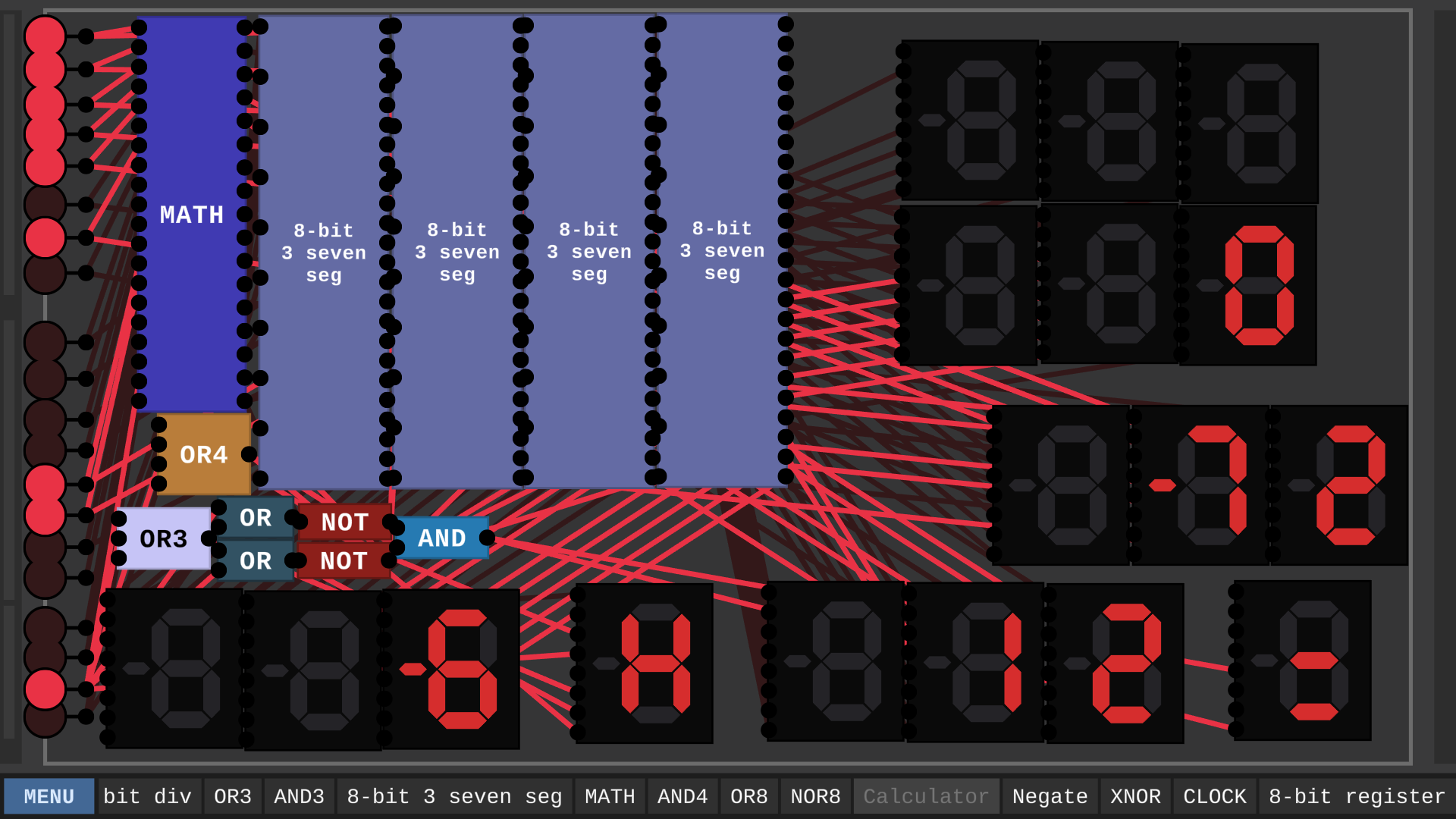
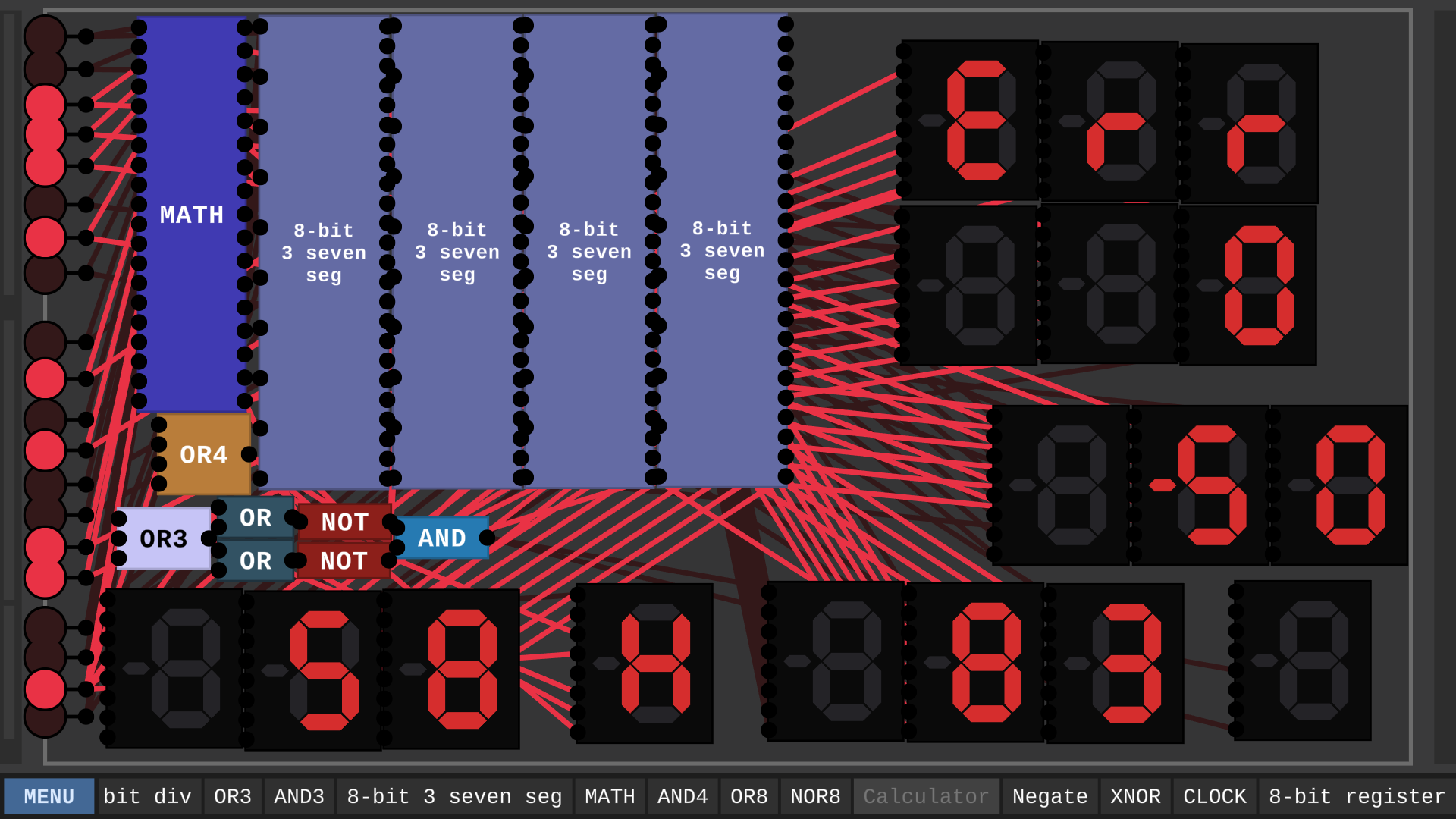
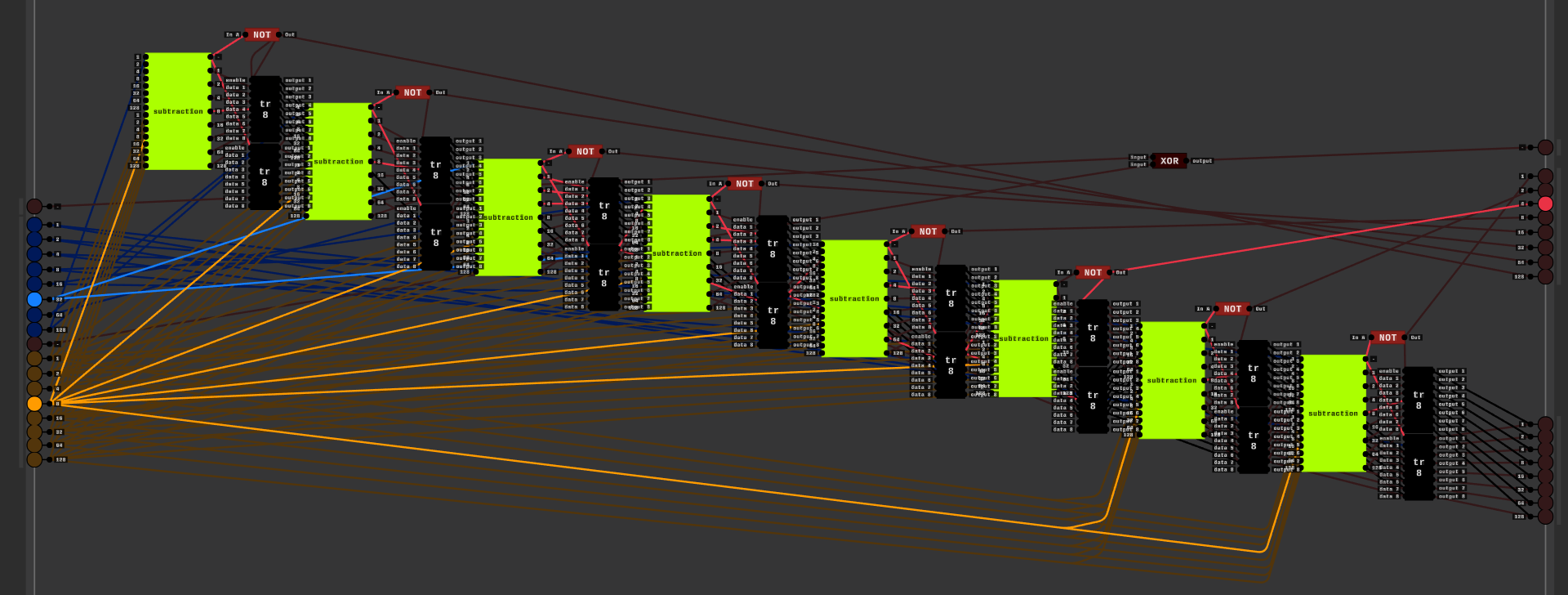
It is finally completed.
This calculator took FOREVER to make. Well, here it is. You put in your numbers select an operation and It gives you an output. The bottom two numbers are your inputs, the one above them is your answer. Above that is your remainder (Only for division.) The last one is the error. It will display "Err" if It detects an error. I think I found all of the errors, but I could have missed some. It is compatible with negatives.
use the long division algorythm:
start by considering only the MSD (most significant digit) of the dividend (blue) by setting it as the LSD (least significant digit) of the remainder and subtracting the divisor (yellow) from it. if the result of the subtraction is not negative then the quotient is at least 128 which means we can set that as the corresponding digit. next left shift your remainder and set the LSD as the next bit of the dividend (64), from here just keep on repeating this process until you have each digit of the quotient, after which the remainder will also be done.
you could, but doing them in parallel makes it a bitwise operation, or in simple people terms: this way the operation completes instantly. this is important because it means you can throw in another input without having to wait for the previous one to finish looping. in traditional division you subtract the divisor from the dividend and count how many times you can subtract before you reach 0 (15 - 5 - 5 - 5 = 0, so 15 / 5 = 3) the long division algorythm takes this operation on numbers and expresses it as an operation on individual digits, the whole point of it is to be bitwise.
