This game, called Qua, uses the words identifying mark as a term to distinguish between sets of game play pieces used by different players. They are also used to distinguish between surfaces on a 3D game board or areas on a topologically equivalent 2D game board that need to be connected as part of a game objective.
The Qua game uses the word cells for places on the game board that can be filled-in with an identifying mark to make a connected chain between a player’s two assigned areas on the game board. For example, an NxNxN game board cube is composed of 1x1x1 cells. Cells are either filled-in with one of three identifying marks, which are also called qua: yellow circles, blue squares and white triangles, or are empty and available for game play.
Qua has a game play rule requiring players to play game play pieces distinguished by their qua identifying mark only in empty cells that connect two already filled-in cells containing their identifying mark, or one such cell and one of their cube faces. The Qua 3D game board does not start out empty. Stratergically located cells are initially filled-in with each players’ qua before the start of a game. This avoids deadlocks and first player unstoppable wins.
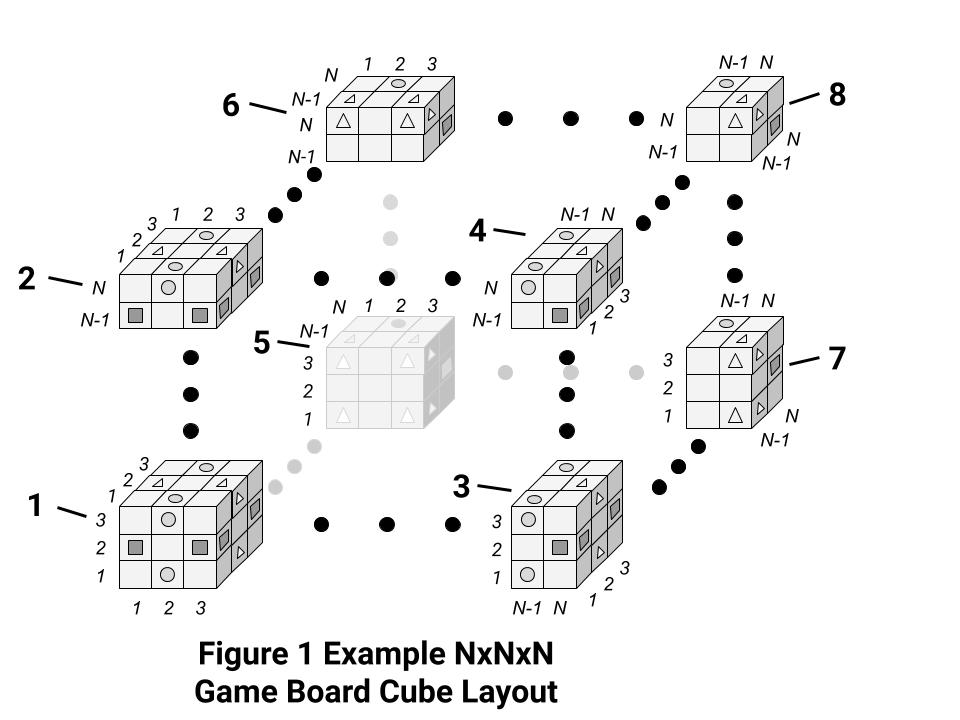
An example Qua game board layout for an NxNxN cube is shown in Figure 1, below. The italicized numbers along the edges of the 1-8 parts of Figure 1 indicate the parallel game play layers in each of three orthogonal directions. Each layer of the Qua Cube game board is composed of cells in the shape of 1x1x1 cubes, where each Qua Cube game board cube face is a layer of NxN cells, each cube edge is composed of N such cells in a straight line, and each cube corner is one such cell. Viewed in any one of the three orthogonal orientations, there are N parallel square layers of NxN cells.
The Qua Cube game board layouts for odd values of N have initial filled-in cells as shown in Figure 1. Although not shown in Figure 1, the left and right Qua Cube faces are associated with circle qua, the top and bottom cube faces are associated with square qua and the front and back cube faces are associated with triangle qua. Part 1 shows the visible qua filled-in cells for the 3x3x3 Qua Cube game board layout, where the middle layer of the 3x3x3 game board in each orthogonal direction has four filled-in cells at the corners, which correspond to the qua associated with the parallel cube faces on either side. The 3x3x3 Qua Cube has a total of 12 cells initially filled-in with qua and 15 cells are empty and available for game play.
Combining parts 2-8 in Figure 1 with part 1, where N=5, shows the visible qua filled-in cells for the 5x5x5 Qua Cube game board layout. Two alternating 5x5 layers parallel to cube faces in each orthogonal direction contain nine filled-in cells: four at the corners, four in the middle of sides and one at the center of these two 5x5 layers, where filled-in cells on each layer contain the qua associated with the corresponding parallel cube faces. For the 5x5x5 Qua Cube game board, 54 cells (2x9=18 cells for each qua) are initially filled-in and 71 cells are empty and available for game play.
Using parts 2-8 for N=7 in Figure 1 to add two additional layers in all three orthogonal directions shows the visible filled-in cells for the 7x7x7 Qua Cube game board layout. Three alternating 7x7 layers parallel to cube faces in each orthogonal direction contain sixteen filled-in cells separated from each other by one empty cell and arranged as 4x4 squares, where filled-in cells on each layer contain the qua associated with the corresponding parallel cube faces. For the 7x7x7 Qua Cube game board, 144 cells (3x16=48 cells for each qua) are initially filled-in and 199 cells are empty and available for game play.
An example Qua Cube game board layout for N=4, where the 4x4x4 Qua Cube is transformed into a 2D playsheet using circles, squares and triangles is one of the downloads in this project. Initially, 30 of the 64 cells in this example 4x4x4 Qua Playsheet are filled-in and 34 are empty and available for game play. Two filled-in cells for each qua are in the center eight internal cells of the visualized Qua Cube, are adjacent to each other to form a chain, are parallel to their associated cube faces, and are perpendicular to the other chains of qua filled cells located in the center eight internal cells. The two-cell circle chain is perpendicular to the square qua cube faces, the square chain is perpendicular to the triangle qua cube faces and the triangle chain is perpendicular to the circle qua cube faces.
Here is the link to this project: https://quagamer.itch.io/qua.