Cool,
I had some tricks on my sleeves, for both conversion and arithmetics.
Therefore, would you extend your VM to support 32-bit arithmetics?
I hadn't looked myself into JackVM yet,
and I'm just gonna share what I have, just in case you need it 😄
Implementing 32-bit addition and subtraction is tricky, but, hang in there!
For these routines, you had to arrange your operands as:
########################################################################### # 32-bit, in big-endian e.g v0 v1 v2 v3 v0 v1 v2 v3 # | v0 v1 v2 v3 | OPERAND A 0x12 0x34 0x56 0x78 0x12 0x34 0x56 0x78 # | v4 v5 v6 v7 | OPERAND B 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF # |===============| =v0===v1===v2===v3= + =v0===v1===v2===v3= - # | v0 v1 v2 v3 | RESULT 0x12 0x34 0x56 0x77 0x12 0x34 0x56 0x79 ########################################################################### # 24-bit, in big-endian e.g v0 v1 v2 v0 v1 v2 # | v0 v1 v2 | OPERAND A 0x12 0x34 0x56 0x12 0x34 0x56 # | v4 v5 v6 | OPERAND B 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF # |===============| =v0===v1===v2= + =v0===v1===v2= - # | v0 v1 v2 | RESULT 0x12 0x34 0x55 0x12 0x34 0x57 ########################################################################### # 16-bit, in big-endian e.g v0 v1 v0 v1 # | v0 v1 | OPERAND A 0x12 0x34 0x12 0x34 # | v4 v5 | OPERAND B 0xFF 0xFF 0xFF 0xFF # |===============| =v0===v1= + =v0===v1= - # | v0 v1 | RESULT 0x12 0x33 0x12 0x35 ########################################################################### # 8-bit e.g v0 v0 # | v0 | OPERAND A 0x12 0x12 # | v4 | OPERAND B 0xFF 0xFF # |===============| =v0= + =v0= - # | v0 | RESULT 0x11 0x17 ###########################################################################
This is the whole 32-bits, 24-bits, 16-bits, and 8-bits addition routine within only 24 bytes!
# Carry Operand A : car32 v2 += vF : car24 v1 += vF : car16 v0 += vF ; # Add Operand A by Operand B : add32 v3 += v7 car32 : add24 v2 += v6 car24 : add16 v1 += v5 car16 : add8 v0 += v4 ;
For subtraction, it's another story...
Chip-8's subtraction flag is already stupid, and I couldn't think a way around beside this.
Both subtraction and reversed subtraction, 8-bits, 16-bits, 24-bits, 32-bits, 78 extra bytes!
# Reversed Carry Operand A : ccr32 v2 -= vF : ccr24 v1 -= vF : ccr16 v0 -= vF ; # Decrement Operand A : dec32 v3 -= 1 if v3 == 255 begin : dec24 v2 -= 1 if v2 == 255 begin : dec16 v1 -= 1 if v1 == 255 then : dec8 v0 -= 1 end end ; # Subtraction ( A - B ) : sub32 dec24 v3 -= v7 car32 : sub24 dec16 v2 -= v6 car24 : sub16 dec8 v1 -= v5 car16 : sub8 v0 -= v4 ; # Reversed subtraction ( B - A ) : rsb32 vF := 1 car32 v3 =- v7 crr32 : rsb24 vF := 1 car24 v2 =- v6 crr24 : rsb16 vF := 1 car16 v1 =- v5 crr16 : rsb8 v0 =- v4 ;
Well...
If you want only 32-bit addition / subtraction, they could be simply written as:
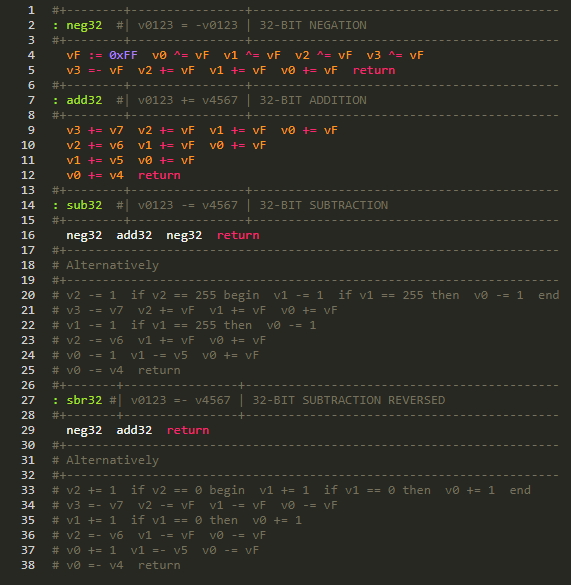
There's still room for improvements for the code I had shown here,
and the redundancies being there is for the sake of readability...
I knew you can optimize it. 😉

