Utilities/Libraries

A topic by Josh Goebel created Sep 17, 2022 Views: 409 Replies: 10

Viewing posts 1 to 9

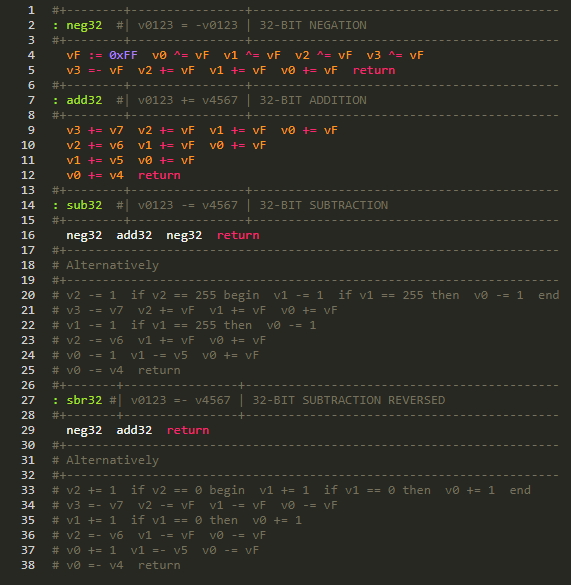
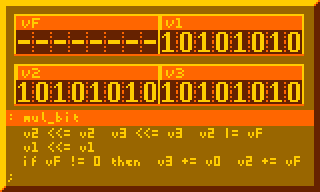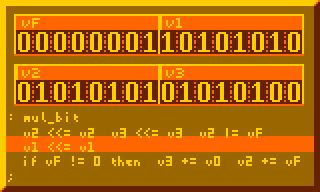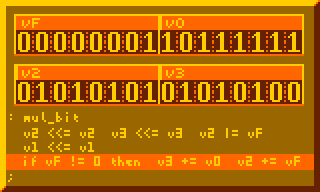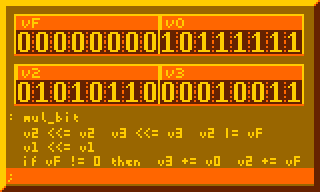
Any interest in utilities/library code for more ambitious XO-Chip projects? I was imagining perhaps a graphics library (circles, lines, etc) or a really nice credits scroller. If anyone is interested in such “support” items I might have some time to help out. Often what I do for this jam is get super excited about a new idea and then build the idea instead of a game anyways. So perhaps I should just realize that that but then help out someone else’s project.

Thoughts?

For my own game (if I have time) I’m thinking of like a scrolling shooter Star Trek game or story based platformer. I’m (mostly) interested in XO-Chip turned way up (ludicrous) to try and build something but if I thought of something slower I could imagine trying more “realistic” speeds (probably still XO though for the RAM).

TimendusSubmitted2 years ago

Sounds like an interesting idea! I'm sure there are already quite a few useful snippets of code out there, maybe a fun community project could be to collect and index those somewhere. I have some in-memory masked sprite drawing routines in my entry from last year, to contribute.

Concerning graphics primitives: most people try to target the older systems, or something "spiritually compatible" with those clock speeds. As such, when you need a circle, you pre-draw a circle and store that as sprites, because computationally drawing a circle is just way too slow :D But nevertheless, having line/circle/square drawing routines is probably useful for someone targeting XO-CHIP.

KouzerumatsukiteSubmitted2 years ago (1 edit)

I had interest on implementing some sort of arithmetic routines for CHIP-8; either or not uses XO-CHIP extension, but might provide two versions (vanilla and XO-CHIP). I got a dream to have basic raytracing implemented in this system, ignoring on how long it would take to compute, at least without throttling the emulation speed...

TimendusSubmitted2 years ago

Yes, I had the same idea. CHIP-8 could probably do with a good fixed-point math library more than it could do with graphics primitives :)

KouzerumatsukiteSubmitted2 years ago

Having fixed point arithmetics in CHIP-8 would been good idea haha, it's just way easier to do than doing floating points 👀

And at the same time, not only fixed point, but string conversion of it as well, either fixed point to string or vice versa, just for convenience.

Umm... I'm still unsure how to make this compatible for the ongoing Jack/NAND2Tetris, esp for the string conversion...

Josh Goebel2 years ago (1 edit)

If you’re referring to my thread Jack (as defined by the course) doesn’t support floats, only int16/bool/array objects that contain those things. You could of course write a floating point library in Jack, but it doesn’t have operator overloading and such niceties… or you could add it to the language/compiler itself and write it in Jack VM opcodes (or even Chip8 instructions). I haven’t gotten that far - I’m still finishing the VM.

Fixed floats would be easily compatible with 16-bit math, right? The fastest code to run natively would be code that just treated it as one big 16 bit number with a virtual decimal. If so then all the 16-bit math in the Jack VM (and the OS multiply/divide routines) would “just work” out of the box…

The only trick would come at the edges when you needed strings or just the integer or fractional components. You could potentially even use a lookup table for converting the fractional remainder to a base10 number, then feed it into the existing BCD to font stuff.

Where were people imagining the fixed point being?

KouzerumatsukiteSubmitted2 years ago (1 edit)

Fixed floats, ehm, fixed points, is fractional numbers, which is being stored as integer.

Let's say, in currency, to represent 0.99, just store it as 99; or 1.25, just store it as 125.
Divide them by 100 when you want to display it, or when doing multiplication on them.
And you don't need to divide them when doing addition or subtraction on them.

The same principle applied to binary:
storing 0b1010.101 (10.625) as 0b1010101 (85),
which later divided by 0b1000 (8) since 3 bits are the fraction parts. or
storing 0b111.1111 (7.9375) as 0b1111111 (127),
which is later divided by 0b10000 (16) since 4 bits are the fractions.

In here, you have to determine how much bits you gonna sacrifice to store fractions,
in this case, you gonna have 8 bits integers, 8 bits of fractions, totaling of 16bits number
you gonna have the granularity of 1/256 (0.00390625) which in binary 0b00000000.00000001
and the largest number you can represent with this would be
65535/256 (255.99609375) a.k.a 0b11111111.11111111

KouzerumatsukiteSubmitted2 years ago (2 edits)

Any how, you don't need look up table to convert 16-bit fixed points into decimal 😄

The shortest and fastest code for 16-bit fixed points to decimal conversion
that I had come up with would be:

: zeroes
  0 0 0 0 0 0 0 0 0 0 0 0
: decimal_result
  0 0 0
: decimal_fractional_part
  0 0 0 0 0 0 0 0 0
: convert_16_bit_fixed_point_to_decimal
# v0 : Hi-byte
# v1 : Lo-byte
  i := decimal_result  bcd v0
  vF := v1  i := zeroes  load v8  v0 := vF
  # extract decimal of the whole 8-bits
  decimal_extract_bit
  decimal_extract_bit
  decimal_extract_bit
  decimal_extract_bit
  decimal_extract_bit
  decimal_extract_bit
  decimal_extract_bit
  decimal_extract_bit
  # what font index is a dot point
  v0 := DOT_POINT
  # store the result
  i := decimal_fractional_part
  save v8
return
: decimal_extract_bit
# performs reverse double-dabble
  v0 >>= v0  if vF != 0 then  v1 += 10 
  v1 >>= v1  if vF != 0 then  v2 += 10 
  v2 >>= v2  if vF != 0 then  v3 += 10 
  v3 >>= v3  if vF != 0 then  v4 += 10 
  v4 >>= v4  if vF != 0 then  v5 += 10
  v5 >>= v5  if vF != 0 then  v6 += 10
  v6 >>= v6  if vF != 0 then  v7 += 10
  v7 >>= v7  if vF != 0 then  v8 += 10
  v8 >>= v8
return

KouzerumatsukiteSubmitted2 years ago (7 edits) (+1)

Cool,

I had some tricks on my sleeves, for both conversion and arithmetics.
Therefore, would you extend your VM to support 32-bit arithmetics?

I hadn't looked myself into JackVM yet,
and I'm just gonna share what I have, just in case you need it 😄

Implementing 32-bit addition and subtraction is tricky, but, hang in there!
For these routines, you had to arrange your operands as:

########################################################################### 
# 32-bit, in big-endian   e.g   v0   v1   v2   v3      v0   v1   v2   v3 
# |  v0 v1 v2 v3  | OPERAND A  0x12 0x34 0x56 0x78    0x12 0x34 0x56 0x78 
# |  v4 v5 v6 v7  | OPERAND B  0xFF 0xFF 0xFF 0xFF    0xFF 0xFF 0xFF 0xFF 
# |===============|            =v0===v1===v2===v3= +  =v0===v1===v2===v3= - 
# |  v0 v1 v2 v3  | RESULT     0x12 0x34 0x56 0x77    0x12 0x34 0x56 0x79 
########################################################################### 
# 24-bit, in big-endian   e.g   v0   v1   v2           v0   v1   v2 
# |  v0 v1 v2     | OPERAND A  0x12 0x34 0x56         0x12 0x34 0x56 
# |  v4 v5 v6     | OPERAND B  0xFF 0xFF 0xFF         0xFF 0xFF 0xFF 
# |===============|            =v0===v1===v2= +       =v0===v1===v2= - 
# |  v0 v1 v2     | RESULT     0x12 0x34 0x55         0x12 0x34 0x57 
########################################################################### 
# 16-bit, in big-endian   e.g   v0   v1                v0   v1  
# |  v0 v1        | OPERAND A  0x12 0x34              0x12 0x34 
# |  v4 v5        | OPERAND B  0xFF 0xFF              0xFF 0xFF 
# |===============|            =v0===v1= +            =v0===v1= - 
# |  v0 v1        | RESULT     0x12 0x33              0x12 0x35 
########################################################################### 
# 8-bit                   e.g   v0                     v0 
# |  v0           | OPERAND A  0x12                   0x12 
# |  v4           | OPERAND B  0xFF                   0xFF 
# |===============|            =v0= +                 =v0= - 
# |  v0           | RESULT     0x11                   0x17 
###########################################################################

This is the whole 32-bits, 24-bits, 16-bits, and 8-bits addition routine within only 24 bytes!

# Carry Operand A  
: car32  v2 += vF  
: car24  v1 += vF  
: car16  v0 += vF  
;  
# Add Operand A by Operand B  
: add32  v3 += v7  car32  
: add24  v2 += v6  car24  
: add16  v1 += v5  car16  
: add8   v0 += v4  
;

For subtraction, it's another story...

Chip-8's subtraction flag is already stupid, and I couldn't think a way around beside this.
Both subtraction and reversed subtraction, 8-bits, 16-bits, 24-bits, 32-bits, 78 extra bytes!

# Reversed Carry Operand A
: ccr32  v2 -= vF
: ccr24  v1 -= vF
: ccr16  v0 -= vF
;
# Decrement Operand A
: dec32  v3 -= 1  if v3 == 255 begin
: dec24  v2 -= 1  if v2 == 255 begin
: dec16  v1 -= 1  if v1 == 255 then
: dec8   v0 -= 1  end  end
;
# Subtraction ( A - B )
: sub32  dec24  v3 -= v7  car32
: sub24  dec16  v2 -= v6  car24
: sub16  dec8   v1 -= v5  car16
: sub8          v0 -= v4
;
# Reversed subtraction ( B - A )
: rsb32  vF := 1  car32  v3 =- v7  crr32
: rsb24  vF := 1  car24  v2 =- v6  crr24
: rsb16  vF := 1  car16  v1 =- v5  crr16
: rsb8                   v0 =- v4
;

Well...

If you want only 32-bit addition / subtraction, they could be simply written as:

There's still room for improvements for the code I had shown here,
and the redundancies being there is for the sake of readability...
I knew you can optimize it. 😉

KouzerumatsukiteSubmitted2 years ago(+2)

Alrighty, I had multiplication routine on me, and I'm sharing it with sincere here 😊

The routine here follows peasant multiplication algorithm.
The principle is same long multiplication method, which is usually taught on school

The primary multiplication routines

This is the most crucial part for performing multiplication, summing multiplicand to product for every bit of multiplier:

# Per-bit mult sum, primary component of 8-bit mult
: mul_bit
  v2 <<= v2  v3 <<= v3  v2 |= vF
  v1 <<= v1
  if vF != 0 then  v3 += v0  v2 += vF
;

The subroutine above executed 8-times in the 8-bit multiplication routine below:

####################################################
# Full 8-bit multiplication routine (primary)
# 8-bits operands, with 16-bits product
# |     v0   | OPERAND A       0x12  
# |     v1   | OPERAND B       0xFF
# |======= X |            =v2===v3= X
# |  v2 v3   | RESULT     0x11 0xEE
####################################################
: mul8p
# Initialize
  v2 := 0  v3 := 0
# Multiply!
  mul_bit  mul_bit
  mul_bit  mul_bit
  mul_bit  mul_bit
  mul_bit  mul_bit
;

[there is no illustration for this, as creating the animation is pain af]

And yes, 8-bit multiplier, takes both operands in 8-bits, gives 16-bits products.
The first 8-bit of the product is high-byte, the latter 8-bit of the product is low-byte.
Thus, this would be the building blocks to perform 16-bits or 32-bits multiplications. 😄

Alright, there are another primary multiplication subroutines out of the full 8-bit multiplier.
A full 16-bit multiplier!

#####################################################
# Full 16-bit multiplication routine (primary)
# 16-bits operands, with 32-bits product
# |         v0 v1   | OPERAND A            0x12 0x34
# |         v2 v3   | OPERAND B            0xFF 0xFF
# | ============= * |            =v4===v5===v6===v7=
# |   v4 v5 v6 v7   | RESULT     0x12 0x33 0xED 0xCC
#####################################################
: mul16cro         #  Carry out
  v6 += v3  v5 += vF  v4 += vF  v5 += v2  v4 += vF
;
: mul16p
# Backup operands
  i := multmp0  save v3
# Multiply matching parts
  i := multmp0  load v2  v1 := v2  mul8p   v4 := v2  v5 := v3
  i := multmp1  load v2  v1 := v2  mul8p   v6 := v2  v7 := v3 
# Multiply across parts
  i := multmp0  load v3  v1 := v3  mul8p   mul16cro
  i := multmp1  load v2            mul8p   mul16cro
;

aaaand a full 32-bit multiplier:

####################################################################################
# Full 32-bit multiplication routine (primary)
# 32-bits operands, with 64-bits product
# |              v0 v1 v2 v3   | OPERAND A                      0x12 0x34 0x56 0x78
# |              v4 v5 v6 v7   | OPERAND B                      0xFF 0xFF 0xFF 0xFF
# | ======================== * |            =v8===v9===vA===vB===vC===vD===vE===vF=
# |  v8 v9 vA vB vC vD vE vF   | RESULT     0x12 0x34 0x56 0x77 0xED 0xCB 0xA9 0x88
####################################################################################
: mul32crD  vC += vF  #  Carry add from vD
: mul32crC  vB += vF  #  Carry add from vC
: mul32crB  vA += vF  #  Carry add from vB
: mul32crA  v9 += vF  #  Carry add from vA
: mul32cr9  v8 += vF  #  Carry add from v9
;
: mul32cro            #  Carry out
  vD += v7  mul32crD
  vC += v6  mul32crC
  vB += v5  mul32crB
  vA += v6  mul32crA
;
: mul32p
# Backup operands
  i := multmp0  save v7
# Multiply matching parts
  i := multmp0  load v6  v2 := v4  v3 := v5  mul16p  v8 := v4  v9 := v5  vA := v6  vB := v7  
  i := multmp2  load v6  v2 := v4  v3 := v5  mul16p  vC := v4  vD := v5  vE := v6  
# Do special care for the product at vF, since it's always erased
  i := mulbkvf  v0 := v7  save v0
# Multiply across parts
  i := multmp2  load v6                      mul16p  mul32cro
  i := multmp0  load v6  v2 := v5  v3 := v6  mul16p  mul32cro
# Restore the vF of the product
  :next mulbkvf  vF := 0
;

If you find some mistakes, feel free to correct me, I haven't tested the code yet 💀

I'll provide fixed points multiplications out of these.

Josh Goebel2 years ago(+1)

I need to just put all the code on GitHub… I haven’t had a chance to finish it yet or clean it up… but I should find the time to post what I have for anyone who wants to play with it. Personally I don’t consider it super useful without a paired compiler, but perhaps that’s just me.

Therefore, would you extend your VM to support 32-bit arithmetics?

That would require some thought… the stack is currently all 16-bit values… the opcodes that process data all 16-bit, etc… To go all in on 32-bit you’d really need a dedicated series of 32-bit push/pop/math opcodes… I’m using 7 bits to store the opcode though, so that does allow 128 instructions (of which I’m only using 36 or so) - so we would have plenty of space in the instruction set for 8 and 32-bit ops.

Perhaps one could add 32-bit math just by making the stack (largely) agnostic about what it’s storing… if you call push32 push32 mul32… then you are pushed 8 bytes unto the stack and multiplying them as two 32-bit numbers…

I’ll see if I can get what I have so far published by Sun/Mon… it’s at home on my other system though or I’d work on it right now.

itch.io

Octojam 9

Utilities/Libraries

The primary multiplication routines