Alrighty, I had multiplication routine on me, and I'm sharing it with sincere here 😊
The routine here follows peasant multiplication algorithm.
The principle is same long multiplication method, which is usually taught on school
The primary multiplication routines
This is the most crucial part for performing multiplication, summing multiplicand to product for every bit of multiplier:
# Per-bit mult sum, primary component of 8-bit mult : mul_bit v2 <<= v2 v3 <<= v3 v2 |= vF v1 <<= v1 if vF != 0 then v3 += v0 v2 += vF ;
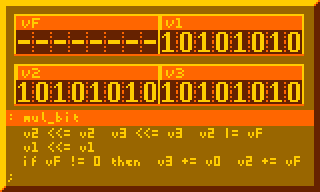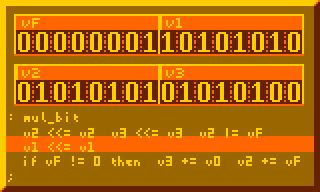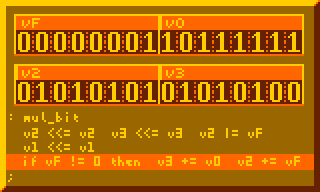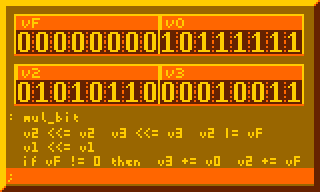
The subroutine above executed 8-times in the 8-bit multiplication routine below:
#################################################### # Full 8-bit multiplication routine (primary) # 8-bits operands, with 16-bits product # | v0 | OPERAND A 0x12 # | v1 | OPERAND B 0xFF # |======= X | =v2===v3= X # | v2 v3 | RESULT 0x11 0xEE #################################################### : mul8p # Initialize v2 := 0 v3 := 0 # Multiply! mul_bit mul_bit mul_bit mul_bit mul_bit mul_bit mul_bit mul_bit ;
[there is no illustration for this, as creating the animation is pain af]
And yes, 8-bit multiplier, takes both operands in 8-bits, gives 16-bits products.
The first 8-bit of the product is high-byte, the latter 8-bit of the product is low-byte.
Thus, this would be the building blocks to perform 16-bits or 32-bits multiplications. 😄
Alright, there are another primary multiplication subroutines out of the full 8-bit multiplier.
A full 16-bit multiplier!
##################################################### # Full 16-bit multiplication routine (primary) # 16-bits operands, with 32-bits product # | v0 v1 | OPERAND A 0x12 0x34 # | v2 v3 | OPERAND B 0xFF 0xFF # | ============= * | =v4===v5===v6===v7= # | v4 v5 v6 v7 | RESULT 0x12 0x33 0xED 0xCC ##################################################### : mul16cro # Carry out v6 += v3 v5 += vF v4 += vF v5 += v2 v4 += vF ; : mul16p # Backup operands i := multmp0 save v3 # Multiply matching parts i := multmp0 load v2 v1 := v2 mul8p v4 := v2 v5 := v3 i := multmp1 load v2 v1 := v2 mul8p v6 := v2 v7 := v3 # Multiply across parts i := multmp0 load v3 v1 := v3 mul8p mul16cro i := multmp1 load v2 mul8p mul16cro ;
aaaand a full 32-bit multiplier:
#################################################################################### # Full 32-bit multiplication routine (primary) # 32-bits operands, with 64-bits product # | v0 v1 v2 v3 | OPERAND A 0x12 0x34 0x56 0x78 # | v4 v5 v6 v7 | OPERAND B 0xFF 0xFF 0xFF 0xFF # | ======================== * | =v8===v9===vA===vB===vC===vD===vE===vF= # | v8 v9 vA vB vC vD vE vF | RESULT 0x12 0x34 0x56 0x77 0xED 0xCB 0xA9 0x88 #################################################################################### : mul32crD vC += vF # Carry add from vD : mul32crC vB += vF # Carry add from vC : mul32crB vA += vF # Carry add from vB : mul32crA v9 += vF # Carry add from vA : mul32cr9 v8 += vF # Carry add from v9 ; : mul32cro # Carry out vD += v7 mul32crD vC += v6 mul32crC vB += v5 mul32crB vA += v6 mul32crA ; : mul32p # Backup operands i := multmp0 save v7 # Multiply matching parts i := multmp0 load v6 v2 := v4 v3 := v5 mul16p v8 := v4 v9 := v5 vA := v6 vB := v7 i := multmp2 load v6 v2 := v4 v3 := v5 mul16p vC := v4 vD := v5 vE := v6 # Do special care for the product at vF, since it's always erased i := mulbkvf v0 := v7 save v0 # Multiply across parts i := multmp2 load v6 mul16p mul32cro i := multmp0 load v6 v2 := v5 v3 := v6 mul16p mul32cro # Restore the vF of the product :next mulbkvf vF := 0 ;
If you find some mistakes, feel free to correct me, I haven't tested the code yet 💀
I'll provide fixed points multiplications out of these.

