itch.io

We can use a different cell size with some relatively small changes. Here's a 6x8 bitmap font I was able to track down:

 

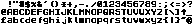
Let's start by generalizing the "Import Sheet" script to adjust "img" to suit the dimensions of the imported bitmap. As an extra precaution to suit this example image, I'll also use image.map[] to convert any white pixels (pattern 32) into transparent pixels (pattern 0):

on click do
 i:read["image"].map[32 dict 0]
 img.size:i.size
 img.paste[i]
end

Note that the size of images and widgets (the .size attribute) is given as a (width,height) pair instead of as separate ".x" and ".y" fields. In Lil, arithmetic operators like + and * generalize to work between single numbers (scalars) and lists of numbers:

These operators also generalize to work between two lists, pairing up every corresponding element of the lists:

(2,3)+(10,20)    # (12,23)

Given the size of an image, if we assume three rows of 32 characters, we can compute the cell size with a single division:

cell:img.size/(32,3)     # (6,8)

This process of generalization between numbers and lists of numbers is called "Conforming", and is described in more detail in the Lil reference manual.

In our "Create" button's script, we use the "cross" operator to create a list of coordinate pairs for every cell of the grid:

32 cross 3
# ((0,0),(1,0),(2,0),(3,0),(4,0),(5,0),(6,0),(7,0),(8,0),(9,0),(10,0),(11,0),(12,0),(13,0),(14,0),(15,0),(16,0),(17,0),(18,0),(19,0),(20,0),(21,0),(22,0),(23,0),(24,0),(25,0),(26,0),(27,0),(28,0),(29,0),(30,0),(31,0),(0,1),(1,1),(2,1),(3,1),(4,1),(5,1),(6,1),(7,1),(8,1),(9,1),(10,1),(11,1),(12,1),(13,1),(14,1),(15,1),(16,1),(17,1),(18,1),(19,1),(20,1),(21,1),(22,1),(23,1),(24,1),(25,1),(26,1),(27,1),(28,1),(29,1),(30,1),(31,1),(0,2),(1,2),(2,2),(3,2),(4,2),(5,2),(6,2),(7,2),(8,2),(9,2),(10,2),(11,2),(12,2),(13,2),(14,2),(15,2),(16,2),(17,2),(18,2),(19,2),(20,2),(21,2),(22,2),(23,2),(24,2),(25,2),(26,2),(27,2),(28,2),(29,2),(30,2),(31,2))

Instead of scaling every number in this list of pairs by 8, we now want to scale the first of each of these pairs by 6 and the second of each of these pairs by 8.

The "flip" operator transposes the x and y axes of a matrix (a list of lists). Given a list of (x,y) pairs, it produces a pair of lists: the first containing x coordinates, the second containing y coordinates:

flip 32 cross 3
# ((0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31),(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2))

We can then multiply this pair of lists by our cell size, and then "flip" again to turn them back into a list of (x,y) pairs. In a more conventional language you'd probably have to write a loop (or two) to built this list of coordinates. Learning to use conforming to your advantage is the secret to concise and fast Lil.

cell * flip 32 cross 3
# ((0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96,102,108,114,120,126,132,138,144,150,156,162,168,174,180,186,0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96,102,108,114,120,126,132,138,144,150,156,162,168,174,180,186,0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96,102,108,114,120,126,132,138,144,150,156,162,168,174,180,186),(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16))
flip cell * flip 32 cross 3
# ((0,0),(6,0),(12,0),(18,0),(24,0),(30,0),(36,0),(42,0),(48,0),(54,0),(60,0),(66,0),(72,0),(78,0),(84,0),(90,0),(96,0),(102,0),(108,0),(114,0),(120,0),(126,0),(132,0),(138,0),(144,0),(150,0),(156,0),(162,0),(168,0),(174,0),(180,0),(186,0),(0,8),(6,8),(12,8),(18,8),(24,8),(30,8),(36,8),(42,8),(48,8),(54,8),(60,8),(66,8),(72,8),(78,8),(84,8),(90,8),(96,8),(102,8),(108,8),(114,8),(120,8),(126,8),(132,8),(138,8),(144,8),(150,8),(156,8),(162,8),(168,8),(174,8),(180,8),(186,8),(0,16),(6,16),(12,16),(18,16),(24,16),(30,16),(36,16),(42,16),(48,16),(54,16),(60,16),(66,16),(72,16),(78,16),(84,16),(90,16),(96,16),(102,16),(108,16),(114,16),(120,16),(126,16),(132,16),(138,16),(144,16),(150,16),(156,16),(162,16),(168,16),(174,16),(180,16),(186,16))

Here's a complete modified script for the "Create" button that should work for any size of monospaced font with the correct 32x3 grid:

on click do
 cell:img.size/(32,3)
 f:deck.add["font" cell name.text]
 f.space:0
 each p i in flip cell * flip 32 cross 3
  f[i]:img.copy[p cell]
 end
 f[95]:image["%%IMG0AAgACAAAAAAAAFQA"]
 view[]
end

Does that help?