Calculus and analysis
Main articles: Calculus and Mathematical analysis
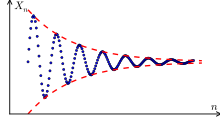
A Cauchy sequence consists of elements that become arbitrarily close to each other as the sequence progresses (from left to right).
Calculus, formerly called infinitesimal calculus, was introduced independently and simultaneously by 17th-century mathematicians Newton and Leibniz. It is fundamentally the study of the relationship of variables that depend on each other. Calculus was expanded in the 18th century by Euler with the introduction of the concept of a function and many other results. Presently, "calculus" refers mainly to the elementary part of this theory, and "analysis" is commonly used for advanced parts.
Analysis is further subdivided into real analysis, where variables represent real numbers, and complex analysis, where variables represent complex numbers. Analysis includes many subareas shared by other areas of mathematics which include:
- Multivariable calculus
- Functional analysis, where variables represent varying functions;
- Integration, measure theory and potential theory, all strongly related with probability theory on a continuum;
- Ordinary differential equations;
- Partial differential equations;
- Numerical analysis, mainly devoted to the computation on computers of solutions of ordinary and partial differential equations that arise in many applications.
Discrete mathematics
Main article: Discrete mathematics

A diagram representing a two-state Markov chain. The states are represented by 'A' and 'E'. The numbers are the probability of flipping the state.
Discrete mathematics, broadly speaking, is the study of individual, countable mathematical objects. An example is the set of all integers. Because the objects of study here are discrete, the methods of calculus and mathematical analysis do not directly apply.<c]<="" a=""> Algorithms—especially their implementation and computational complexity—play a major role in discrete mathematics.</c]<="">
The four color theorem and optimal sphere packing were two major problems of discrete mathematics solved in the second half of the 20th century. The P versus NP problem, which remains open to this day, is also important for discrete mathematics, since its solution would potentially impact a large number of computationally difficult problems.
Discrete mathematics includes:
- Combinatorics, the art of enumerating mathematical objects that satisfy some given constraints. Originally, these objects were elements or subsets of a given set; this has been extended to various objects, which establishes a strong link between combinatorics and other parts of discrete mathematics. For example, discrete geometry includes counting configurations of geometric shapes
- Graph theory and hypergraphs
- Coding theory, including error correcting codes and a part of cryptography
- Matroid theory
- Discrete geometry
- Discrete probability distributions
- Game theory (although continuous games are also studied, most common games, such as chess and poker are discrete)
- Discrete optimization, including combinatorial optimization, integer programming, constraint programming



